比奥固结理论
太沙基固结理论和比奥固结理论是现在zui常用的两种固结理论���,众多学者从理论构架、数值模拟、试验剖析等方面临这两种固结理论举行了深人的剖析���。
太沙基固结理论优点是求解利便���,且其一维固结理论已被普遍应用于地基固结度的盘算与展望���,积累了富厚的工程应用履历���。
但在三维条件下���,因其假设了三个正交偏向正应力之和不随时间转变���,与现实矛盾���,使得所求解并不jing确���。
而比奥固结理论则对其举行了刷新���,阻止了此种有缺陷的假设���。但比奥固结理论增添求解jing确性的同时亦增添了未知参数、提高了求解难度���,使得该理论难以完全剖析���,在实践中应用较为难题���。
由此可见���,两种固结理论各有优势和缺乏���。
比奥固结方程的基本框架是相当清晰明晰的���,方程建设首先基于一样平常弹塑性力学的平衡、几何和物理三大方程假设(如式6-12、6-13、6-14所示)���。应该可以看到这个架构和太沙基头脑略有差别���,其建模自己并没有显示出为解决固结排水而专设的特色���。?

其中���,式(6-12)为平衡方程���,式(6-13)为几何方程���,式(6-14)为物理方程���。
关于这些方程���,人们能够加以刷新亦或立异的水平是差别的���,这是学者们在解决相关问题和获得求解问题便捷性时需注重的一点���。
详细而言���,作为平衡方程的式(6-12)���,着实是一个万neng定律���,人们无法改变���,可是在有水保存的条件下���,应将总应力体现成为有用应力和孔压的组合形式(这样所谓平衡的受力工具依然是土体而不是土粒���,请务必注重这个问题)���;
关于几何方程式(6-13)���,比奥方程一样平常只是取了一阶偏导���,这说明只有在小应变下才华适用���;
而剩下的物理方程(或者在弹塑性力学中称之谓本构方程)���,例如式(6-14)反应的广义虎克定律(这是现在zui为常用的比奥固结方程本构方程)���,则是三大方程中受履历因素(或者说人为因素)影响zui大���,成为求解问题变数zui大的焦点所在���。
比奥方程���,在干土中也可以适用���。而当有孔隙水压力保存时���,即便不思量未知的水平向位移应力分量的个数(仅盘算竖向变形分量)���,方程数仍显着少于未知参数���,这导致纵然是线性方程组都难以求解���,更不必说这是一组令人头疼的偏微分方程了���。
因此真要从比奥法思绪解决固结问题���,除了式(6-12)、式(6-13)、式(6-14)以外���,还要凭证水流量转变���,从引起试样体变这样一个物质守恒的角度���,引入式(6-15)的表达式���,即所谓一连性方程:?
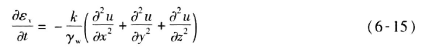
上述架构在一定的本构理论框架(好比线弹性情形)中是严谨的���,然而用这种要领仍难获得可操作性的解答���。因此人们就想到用变通的方法来求解���,zui直接的思绪就是理清这些方程为谁而设——纵然是zui一样平常的三维条件���,针对固结问题���,也并非要求解所有分量���,人们zui想相识的就是孔压消逝历程���,并用其去求解固结度(虽然现实中压缩模量不恒定情形下���,应变固结度与孔压固结度并不统但较之应变���,孔压更容易求解���,并且当压缩模量能够被假设为常数时���,孔压固结度应与位移(应变)固结度一致)���。
为了求解孔压���,在三维条件下���,可通过建设一个体变的物理方程或相关变体���,作为体积转变与孔压转变联系的纽带���,因此便很自然地想到把三个正应变求解的物理方程叠加���,获得式(6-16):
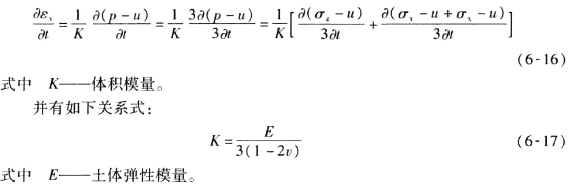
这即是目今运用比奥固结法求解孔压时���,所接纳的较为适用的方程式���。
而式(6-16)也正是太沙基三维固结理论所用到的物理方程���。也许站在今天的视角���,有人会以为太沙基法只是比奥要领的一种重组形式���。
但从历史历程来看���,太沙基固结理论先于比奥固结理论���,他是一步到位地提出了(6-16)这个方程���,这也体现了一切太沙基要领所带有的鲜明烙印——在太沙基的理念中���,工程问题的解答不可只是提出ji难求解的方程���,而让各人去浏览数学之美���;确保在理论性与实践性取得平衡的条件下���,一针见血地解决现实问题的主要矛盾才是追求的至上目的���。
当今比奥固结方程虽然已经被奉为小变形固结理论盘算的圣经级公式���,可是其在求解中的难度���,也使得应用者望而却步���。相比而言���,太沙基方程求解容易���,更有亲和力���,但其三维条件下的解答也保存不jing确的问题���,因此在应用中需审慎选择���。
相识更多产品信息���,获取产品资料���,接待垂询TIPTOP乐虎国际
效劳热线 | 400-633-0508? ? 邮箱:tiptop@tiptoptest.com